深入理解计算机系统（二）—— 整数表示

2.2 整数表示

2.2.1 整型数据类型

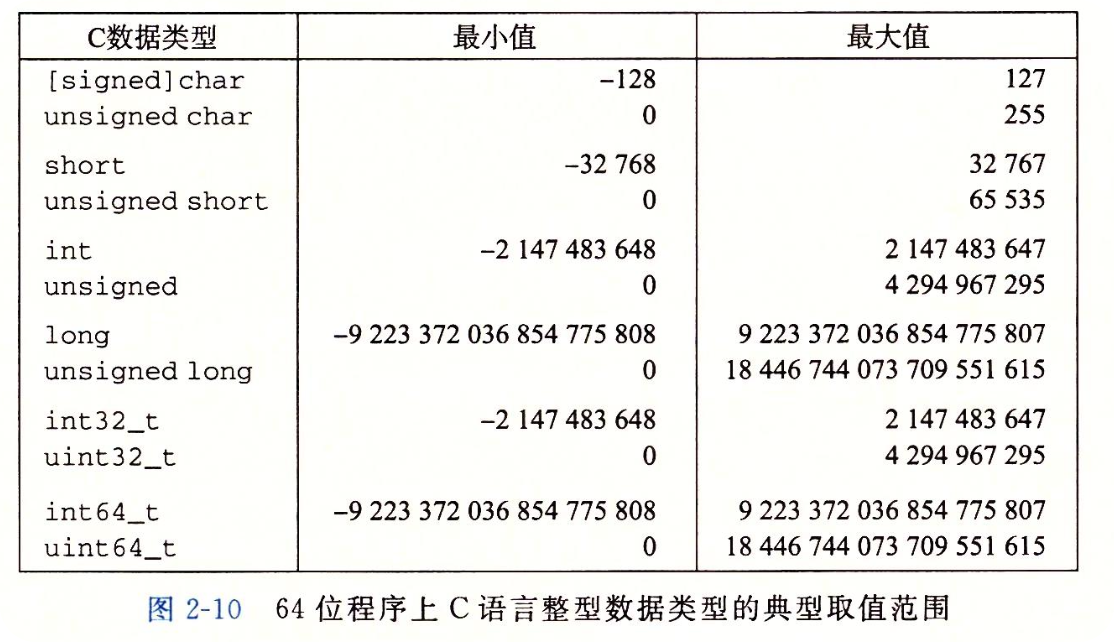
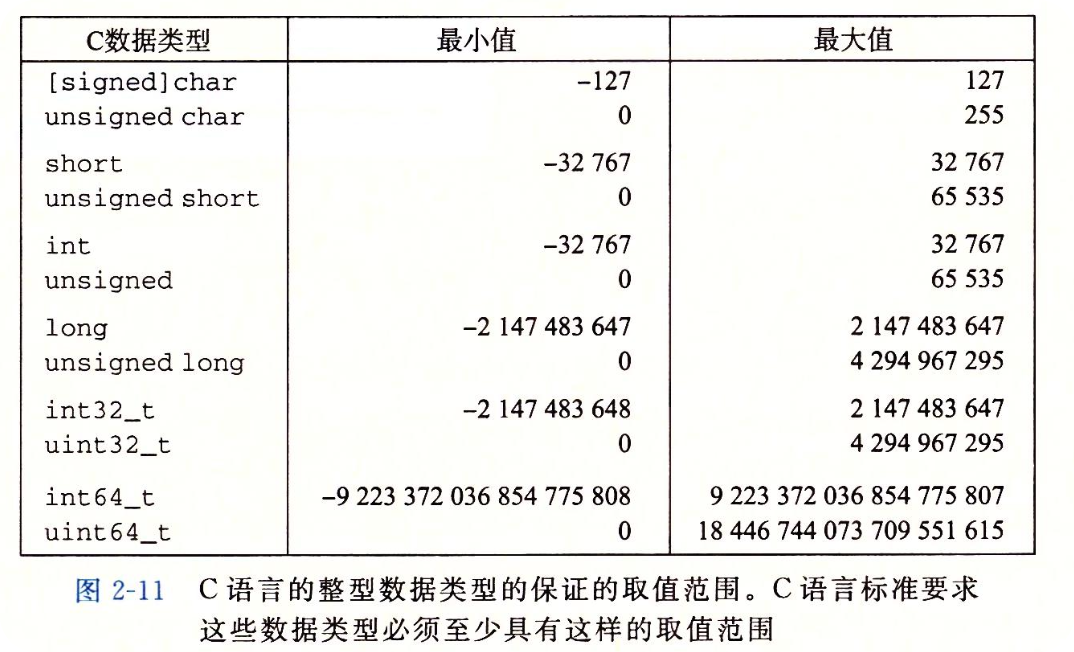
2.2.2 无符号的编码

2.2.3 补码编码

补码编码用于表示负整数。

原码,补码,反码概念和计算方法详解：https://www.itheima.com/news/20200116/103436.html

2.2.4 有符号数和无符号数之间的转换

#include<stdio.h> 

int main() {
	short int v = -123456;
	unsigned short uv = (unsigned short) v;
	printf("v = %d, uv = %u\n", v, uv);
	return 0;
}

上面的代码使用GCC编译运行结果为v = -12345, uv = 53191，有意思的是，当我输出这两个数的十六进制时，得到的结果是完全一样的。

#include <stdio.h>

void show_hex(short int x) {
    printf("十六进制表示: 0x%.4x\n", (unsigned short)x);
}

int main() {
    short int v = -12345;
    unsigned short uv = (unsigned short) v;
    printf("v = %d, uv = %u\n", v, uv); // 这个例子很好的解释了为什么需要格式说明符

    show_hex(v);
    show_hex(uv);

    return 0;
}

输出结果为：

1
2
3

v = -12345, uv = 53191
十六进制表示: 0xffffcfc7
十六进制表示: 0xffffcfc7

原因是：
在16位系统中，这两个数在内存中的位模式完全相同： 1100 1111 1100 0111 (0xCFC7)，区别仅在于解释方式：

作为有符号数时：最高位1表示负数，值为-12345

作为无符号数时：纯二进制值，等于53191

这个现象很好地展示了计算机中数据表示的本质：数据的位模式（binary pattern）是固定的，而其具体值取决于我们如何解释这些位。

2.2.5 C语言中的有符号数与无符号数

尽管C语言标准没有指定有符号数要采用某种方式，但是几乎所有的机器都使用补码。

整型数据在计算机中确实使用补码进行存储。这一设计主要基于以下原因：

统一处理符号位与数字域：补码将符号位（最高位）纳入数值计算，使得正负数的加减法运算可以统一通过加法电路实现，简化了硬件设计

简化运算逻辑：补码通过模运算特性，将减法转换为加法操作。例如，计算 a - b等价于 a + (-b)，而 -b 的补码可直接通过 b 的补码加1得到，避免了额外减法电路的需求。

唯一标识零值：补码消除了原码和反码中存在的“正零”和“负零”问题，确保数值范围覆盖更高效（如8位补码可表示-128到127）。

显式的强制类型转换就会导致数据类型发生变化，如下：

int tx, ty;
unsigned ux, uy;

tx = (int) ux;
uy = (unsigned) ty;

另外，当一种类型的表达式被赋值给另外一种类型的变量时，可能会发生隐式转换，根据赋值运算的隐式转换规则，右侧值会转换为左侧变量的类型，如下，

int tx, ty;
unsigned ux, uy;

tx = ux; // ux 转换为 int
uy = ty; // ty 转化为 unsigned int

当执行一个运算时，如果它的一个运算数时有符号而另一个是无符号的，那么C语言会隐式地将有符号参数强制类型转化为无符号数，并假设这两个数都是非负数。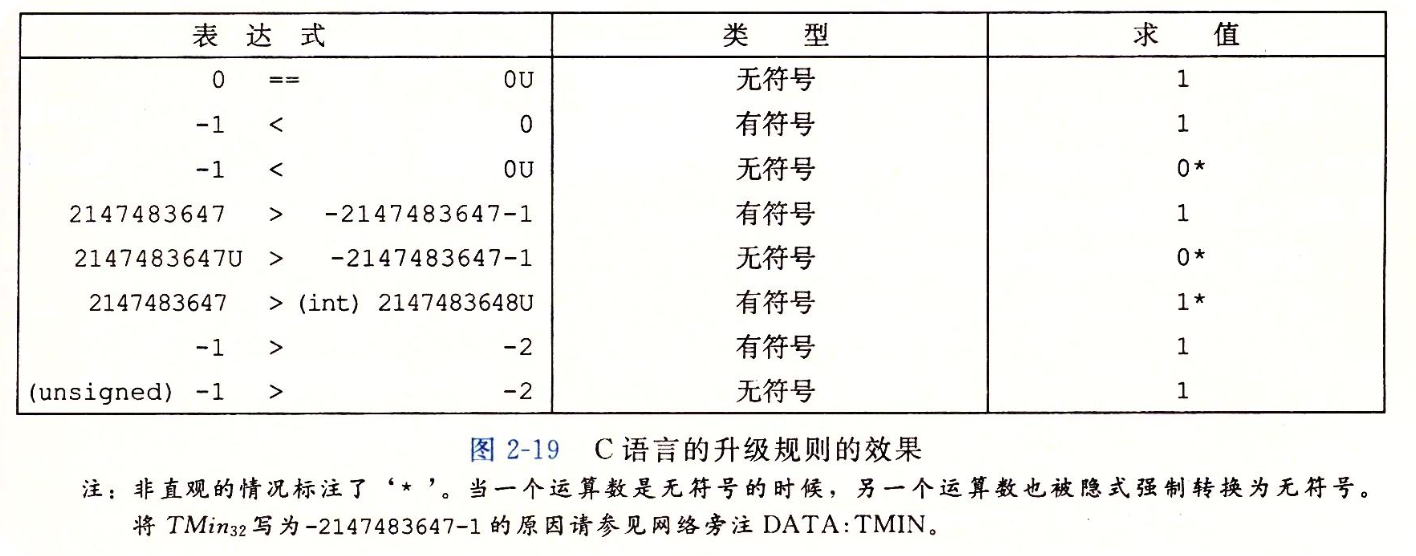

2.2.6 扩展一个数字的位表示

#include <stdio.h>

void show_bytes(unsigned char *start, size_t len) {
    for (int i = 0; i < len; i++) {
        printf("%.2x ", start[i]);
    }
    printf("\n");
}

int main() {
    // 使用位运算模拟不正确的扩展
    short sx = -12345;       
    unsigned short usx = 12345;  
    
    // 错误的扩展方式：直接截断高位字节
    int x_wrong = *(int*)&sx;    // 错误：直接将short的内存解释为int
    unsigned ux_wrong = *(unsigned*)&usx;   // 错误：直接将unsigned short的内存解释为unsigned
    
    // 正确的扩展方式
    int x_correct = sx;      
    unsigned ux_correct = usx;   
    
    // 打印结果对比
    printf("原始短整型值 sx = %d\n", sx);
    printf("错误扩展后 x_wrong = %d\n", x_wrong);
    printf("正确扩展后 x_correct = %d\n", x_correct);
    
    printf("\n原始无符号短整型值 usx = %u\n", usx);
    printf("错误扩展后 ux_wrong = %u\n", ux_wrong);
    printf("正确扩展后 ux_correct = %u\n", ux_correct);
    
    // 打印内存表示
    printf("\nsx的字节表示: ");
    show_bytes((unsigned char*)&sx, sizeof(short));
    
    printf("x_wrong的字节表示: ");
    show_bytes((unsigned char*)&x_wrong, sizeof(int));
    
    printf("x_correct的字节表示: ");
    show_bytes((unsigned char*)&x_correct, sizeof(int));
    
    return 0;
}

位扩展操作确保了在进行类型转换时数字的正确性和运算的准确性，如当小位数类型数据需要转换为大位数类型时（如short转为int） ，错误的扩展可能会将其变成错误的大正数。

这是因为要将一个补码数字转化为一个更大的数据类型，需要执行一个符号扩展，其从小位宽扩展到大位宽，通过符号复制位（最高位）到高位实现。正数的符号位为0，扩展时补0；负数的符号位为1，扩展时补1，以确保数值范围和符号不变。如：

8位有符号数 -64（补码 1100 0000）扩展为16位时，结果为 1111 1111 1100 0000（十进制-64）

而零扩展用于将无符号整数从小位宽扩展到大位宽，通过在高位填充0实现。由于无符号数的所有位均为数值位，补0不会改变数值大小。如：

8位无符号数 0x80（十进制128）扩展为16位时，结果为 0x0080（十进制128）

2.2.7 截断数字

截断数字与位扩展都是不同位宽整数转换的核心操作，与后者相反，截断数字是将一个较大位宽的数值转换为较小位宽时，直接丢弃高位部分，仅保留低位。其本质是模运算（ $mod 2^k$ ），具体规则如下：

1
2
3

int i = 53191;  // 32位补码表示
short j = (short)i;  // 截断为16位，高位丢弃
int k = j;  // 扩展回32位时符号位扩展为1，结果为-12345

无符号数截断：直接对高位进行截断，数值不变。例如，将32位无符号数截断为16位时，直接去掉高16位。

有符号数截断：需先将数值视为无符号数进行截断，再转换为补码形式。例如，截断前符号位为1的补码数，截断后仍保持负数特性。

#include <stdio.h>

int main() {
    int a = 128;      // 32位补码：00000000 00000000 00000000 10000000
    char b = (char)a; // 截断为8位，高位丢弃，保留10000000
    printf("b = %d\n", b); // 输出：-128（补码形式）
    return 0;
}

2.2.8 关于有符号数与无符号数的建议

从上面的各种转化的示例中，不难发现如果我们随意忽略隐式转换，那么很有可能转着转着这个数就失去了其本来的含义，从而引发错误。尤其是有符号数向无符号数的隐式转换，会更容易导致错误和漏洞。

避免这类错误的一种方法就是，绝不使用无符号数。许多语言也是这么设计的，比如Java就天生不支持无符号数。（存在即合理？可能我暂时还用不到吧）